Matrices
Skill Checklist
Track your progress across all skills in your objective. Mark your confidence level and identify areas to focus on.
Track your progress:
Don't know
Working on it
Confident
📖 = included in formula booklet • 🚫 = not in formula booklet
Track your progress:
Don't know
Working on it
Confident
📖 = included in formula booklet • 🚫 = not in formula booklet
Foundations of Matrices
Matrix notation
A matrix is simply a rectangular array of numbers written in rows and columns. For example, the matrix
has 2 rows and 3 columns. We can reference a specific entry using the notation Mi,j where i is the row and j the column. For example, M1,3 is the first row and thirs column, which is π.
Order of a matrix
The order of a matrix denotes its dimensions. We say a matrix has order n×m (read "n by m") to denote that it has n rows and m columns. For example, the matrix
has order 2×3.
Adding & subtracting matrices
When matrices have the same order m×n, we can add or subtract them by simply adding or subtracting the components:
Scalar multiplication of a matrix
We can multiply a matrix by a scalar by simply multiplying each entry by a scalar:
Matrix multiplication
If A has order m×n and B has order n×p, then the product AB is defined and will have order m×p.
Each entry of AB is the dot product of a row of A with a column of B.
For example, if we multiply a 2×2 matrix A by a 2×3 matrix B, the product will be 2×3:
Matrix multiplication is not commutative
In general, for matrices A and B,
Note: this does not mean AB is never equal to BA, just that it is not in general.
Matrix multiplication is associative
For all matrices A,B and C, it is true that
Matrix multiplication is distributive
For all matrices A,B and C, it is true that
Zero Matrix
A matrix with all 0 entries is called the "zero" matrix, regardless of order. We denote it 0.
Matrix math with technology
When you have matrices with only numbers and no parameters (eg k), you can add, multiply, and find powers of matrices using your calculator.
Identity, Inverses & Determinants
Identity Matrix
The identity matrix I is a square matrix with 1s along its top-left to bottom-right diagonal, and 0's everywhere else. When multiplied by any matrix with appropriate order, the product is the same matrix:
Definition of the inverse matrix
The inverse of a matrix is the matrix M−1 that when multiplied by M gives the identity.
Inverse of a 2 by 2 matrix by hand
If M=(acbd), then
Determinant of 2 by 2 matrix by hand
Existence of the inverse
A square matrix M is invertible if and only if its determinant is non-zero:
Operations using inverses: AB=C ⟹ B=A⁻¹C, A=CB⁻¹
If the matrices A and B are invertible, then
Inverse of a matrix using technology
You can find the inverse of any (square) matrix on your calculator. Enter your matrix into your calculator, for example in [A], and then simply type
and the calculator will spit out the inverse, if it exists.
Determinant of a matrix using technology
You can find the determinant of any (square) matrix on your calculator.
Enter your matrix into your calculator, for example in
[A].Under the matrix menu, you will find a bunch of functions, the first of which should be det(. Type
and the calculator will spit out the determinant.
Geometric Transformations with Matrices
2x2 matrix transformation images
A (2×2) matrix M=(acbd) represents a transformation of points in the cartesian plane. For such transformations, we consider x-coordinates in vector form (10), and y-coordinates as (01):
In general, the point (x,y) is transformed to
We call the input to a transformation the object and the output the image.
Transformation scales area by det 𝐌
When a transformation M is applied to a shape, the area of the image is
The absolute value is there as a negative determinant flips the orientation of the object, but that does not change the area.
Geometric enlargement with scale factor k
The matrix M=(k00k) acts as a geometric enlargement with a scale factor k.
Horizontal and vertical stretch by scale factor k
The matrix M=(k001) acts as a geometric stretch with a scale factor k in the horizontal direction.
The matrix M=(100k) acts as a geometric stretch with a scale factor k in the vertical direction.
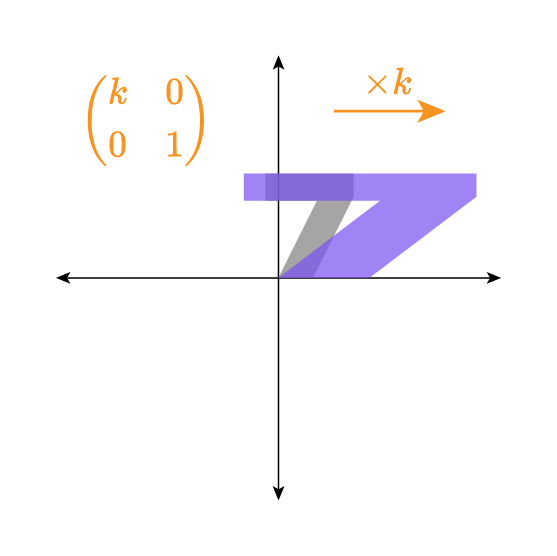
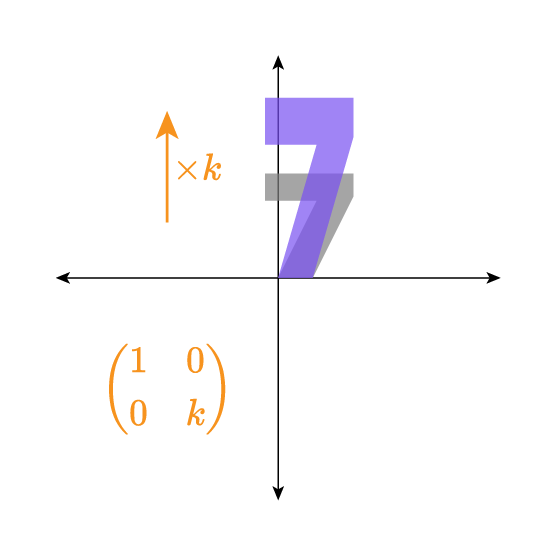
Clockwise and counterclokwise rotation matrices
We can represent rotations about the origin with matrices:
A counterclockwise rotation is represented by (cosθsinθ−sinθcosθ).
A clockwise rotation is represented by (cosθ−sinθsinθcosθ).
![<ul>
<li>A 2D Cartesian coordinate system with horizontal and vertical axes, each shown with arrowheads.</li>
<li>Two congruent polygonal shapes sharing a common vertex at the origin: one gray (positioned in the first quadrant, with a short horizontal top segment and a slanted segment down to the origin) and one purple (rotated into the fourth/third quadrants).</li>
<li>An orange dashed arc with an arrow, drawn clockwise around the origin, labeled θ, indicating the angular relation between the two shapes.</li>
<li>An orange 2×2 matrix displayed at lower left: [ [cos θ, sin θ], [−sin θ, cos θ] ].</li>
</ul>](https://firebasestorage.googleapis.com/v0/b/perplex-learning.appspot.com/o/cheat_sheet%2F1755981851489-c.png?alt=media&token=ef29db09-a780-4111-9009-58ed6c34ee28)
a
Matrix reflection in the line tanθ
The matrix (cos2θsin2θsin2θ−cos2θ) represents a reflection in the line y=xtanθ, which is the line through the origin forming an angle of θ with the positive x-axis.
Translation by a vector
If a point P is translated by a vector (ab), apply a translation a units to the right and b units up:
Composing matrix transformations
Geometric transformations represented by matrices can be chained together, and the combined transformation is represented by the product of the matrices. For example, transformation A then B then C is represented by the matrix (CBA).
Notice that the matrix product has the opposite order from the transformations, since
Systems of equations with Matrices
Writing a system in matrix form
A system of linear equations can be written in matrix form Ax=b. For a system of 3 equations with 3 unknowns, we let x=⎝⎛xyz⎠⎞, and then A is a matrix whose rows are the equations of the system, and columns the coefficients of each variable. The vector b represents the constants on the RHS of the equations.
Solving a system using the inverse
Once a system of equations is written in the form Ax=b, so long as A−1 exists we can find the solution by left-multiplying both sides by the inverse:
This solution is unique.
Interpreting the discriminant for a system of equations
When detA=0, A−1 does not exist. As such, a unique solution does not exist. Instead, the system has either no solutions, or it has infinitely many.
For systems of 2 or 3 equations, this can be interpreted as the lines / planes being parallel, and either lying on top of each other or having no intersections.
Eigenvalues & Eigenvectors
Definition of eigenvectors & eigenvalues
The eigenvectors of a matrix A are the vector(s) v such that
for some constant(s) λ which we call eigenvalues.
Finding Eigenvalues
The eigenvalues λ of a matrix A satisfy
For example, if A=(−1−234) then
which simplifies to
We call λ2−3λ+2 the characteristic polynomial of A.
Finding Eigenvectors
If we know an eigenvalue of a matrix A, we can find the corresponding eigenvector using its definition:
When the matrix A is known, we can solve this system of simultaneous equations to find the eigenvector (xy).
Diagonalizing a matrix
If a matrix A has two distinct, real eigenvalues, then we can write it in the form
where P=(v1v2) is formed with the eigenvectors of A as its columns, and D=(λ100λ2) is a diagonal matrix.